Adventure 1 — Measuring the World (Solution)

Long before satellites and laser measuring tools, no one knew how big the Earth was. People guessed, argued, and made wildly different claims. Some thought the planet was enormous; others believed it was much smaller. What they all agreed on was this: the Earth was far too large to measure directly.

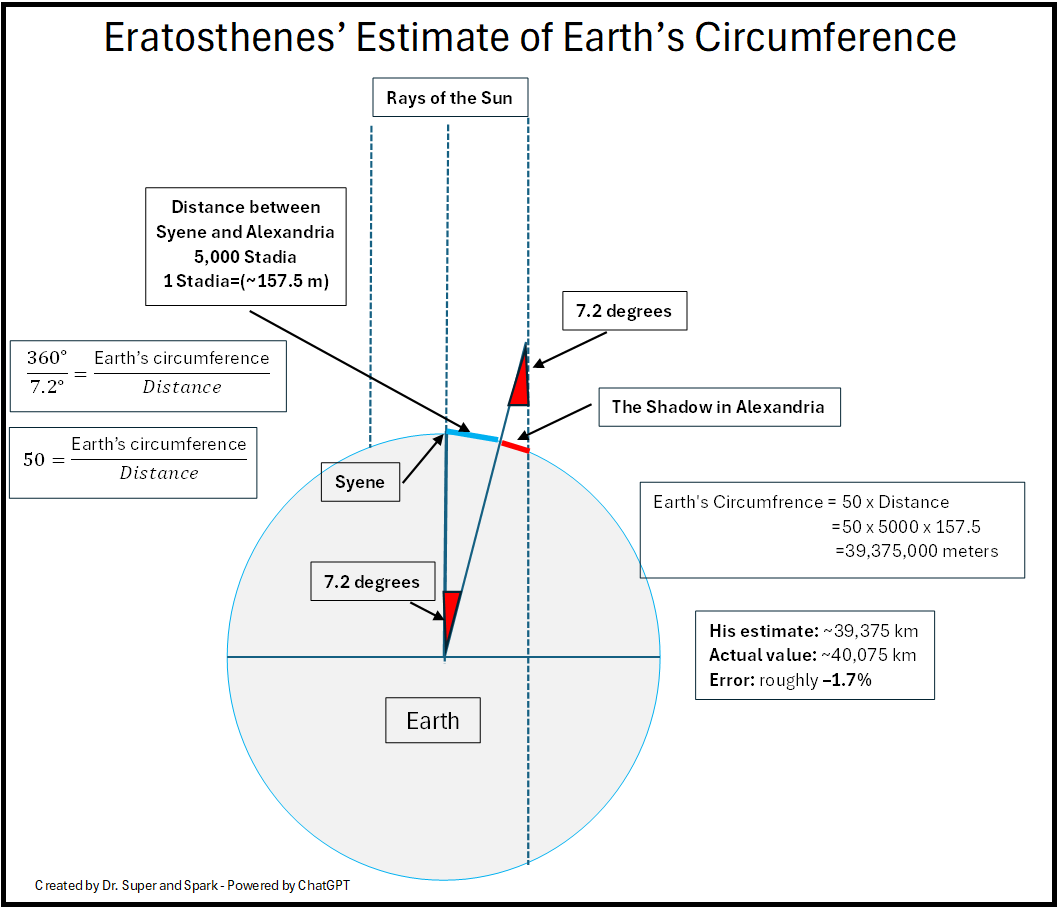
Then came Eratosthenes. He lived more than two thousand years ago and worked in the Great Library of Alexandria — a place filled with scrolls, scholars, and a great deal of sunshine. He heard something curious: in a southern city called Syene, the Sun shone straight down a well on the summer solstice. At the very same moment in Alexandria, a vertical stick cast a small shadow.

This tiny difference — the angle of a single shadow — was the clue. Eratosthenes realized he could “slice” the Earth using shadows the same way we slice area under a line: by taking a simple local measurement and using it to understand something much bigger.

In this activity, you will follow the same idea. You start from the angle θ and the distance D between the two cities, compute the ratio R = C / D, and then work your way to Earth’s circumference in meters and kilometers. Finally, you compare your estimate with a present-day value and see how close you came. The angle θ is the fraction of the full circle between the two cities. The ratio R = C / D tells you how many times that distance D fits around the full Earth. From the geometry of the circle, you can use the relationship R = 360° / θ.

1️⃣ Given angle and distance

Use the diagram to read the value of θ (in degrees). In Eratosthenes’ classic experiment, θ ≈ 7.2°. The distance between Syene and Alexandria along the surface is D meters.

2️⃣ Ratio R = Earth’s circumference / D

Now use the idea above to compute the ratio R. Remember, R tells you how many times the distance D fits around the entire Earth.

R = 360° / θ

3️⃣ Earth’s circumference in meters and kilometers

Once you know D (in meters) and R, you can find the Earth’s circumference in meters using:

Circumference in meters = R × D

Then convert to kilometers by dividing by 1000:

Circumference in kilometers = (circumference in meters) ÷ 1000

4️⃣ Compare with a present-day value

A commonly used present-day value for Earth’s circumference is about 40,075 kilometers.

First, compute the difference between the present-day value and your estimate:

difference = present-day value − your estimate

Then use this difference to find the percent error of your estimate:

percent error = (difference ÷ present-day value) × 100%