✅ Adventure 2 — Solutions
Use this page after you try the activity. It shows the tangent picture, the rise/run idea, and the limit form using
h.
Tip: On the tangent segment, from t=2 to t=4 the run is 2 and the rise is 12.
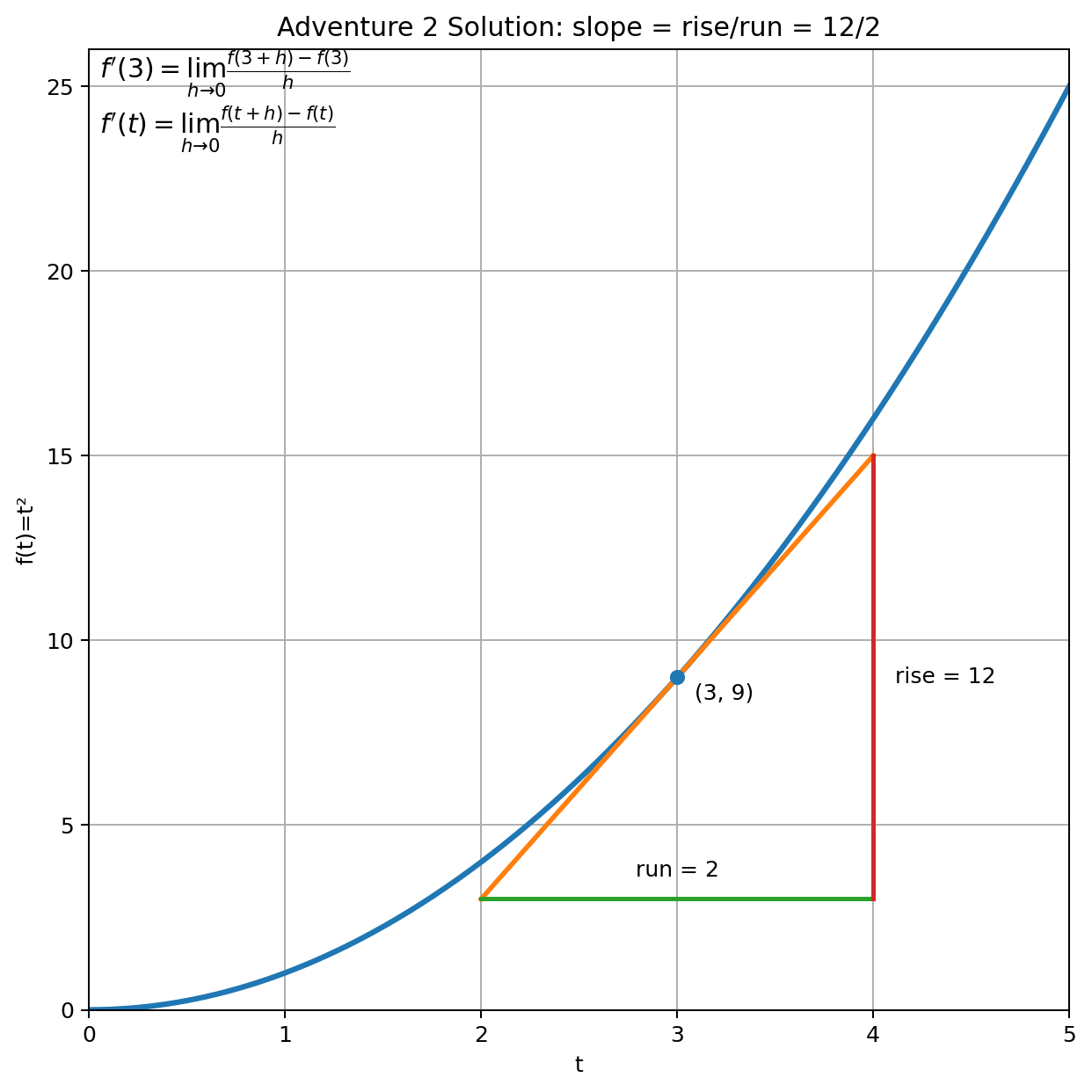
Slope: rise/run = 12/2 = 6.
Difference Quotient at t = 3
f'(3) = lim_(h->0) ( f(3+h) - f(3) ) / h
With f(t)=t^2:
( (3+h)^2 - 9 ) / h = (9 + 6h + h^2 - 9)/h = 6 + h,
so f'(3)=6.
General Rule
f'(t) = lim_(h->0) ( f(t+h) - f(t) ) / h
( (t+h)^2 - t^2 ) / h = (2th + h^2)/h = 2t + h,
so f'(t)=2t.