✏️ Adventure 4 — Activity

Use the charts to connect height, velocity, and acceleration — and discover why calculus is really “slope + area”.

Assumptions: no air resistance • constant acceleration downward • time ticks every 1 second.

✳ Equations (given)

y(t) = 980 − ½ g t²
v(t) = y′(t)
a(t) = v′(t)

1) Height vs Time (Read the graph)

Height after 4 seconds (m):

Height after 10 seconds (m):

Distance fallen from 4 s to 10 s (m):

2) Velocity and Distance (Area under v(t))

Area under v(t) from 0→4 s (m):

Area under v(t) from 0→10 s (m):

Does area match distance fallen? (type Yes or No)

3) Hitting the Ground

Impact time t (s):

Impact speed (m/s):

Impact speed (km/h):

Graph check: type ✅ or ❌

4) Acceleration Check (Area under a(t))

Area under a(t) from 4→10 s (m/s):

Explain (1 sentence):

★ Calculus Challenge (Show your work)

Differentiate y(t) to find v(t). Differentiate again to find a(t).
Could you recover v(t) and y(t) by integrating a(t) and v(t)? Explain briefly.

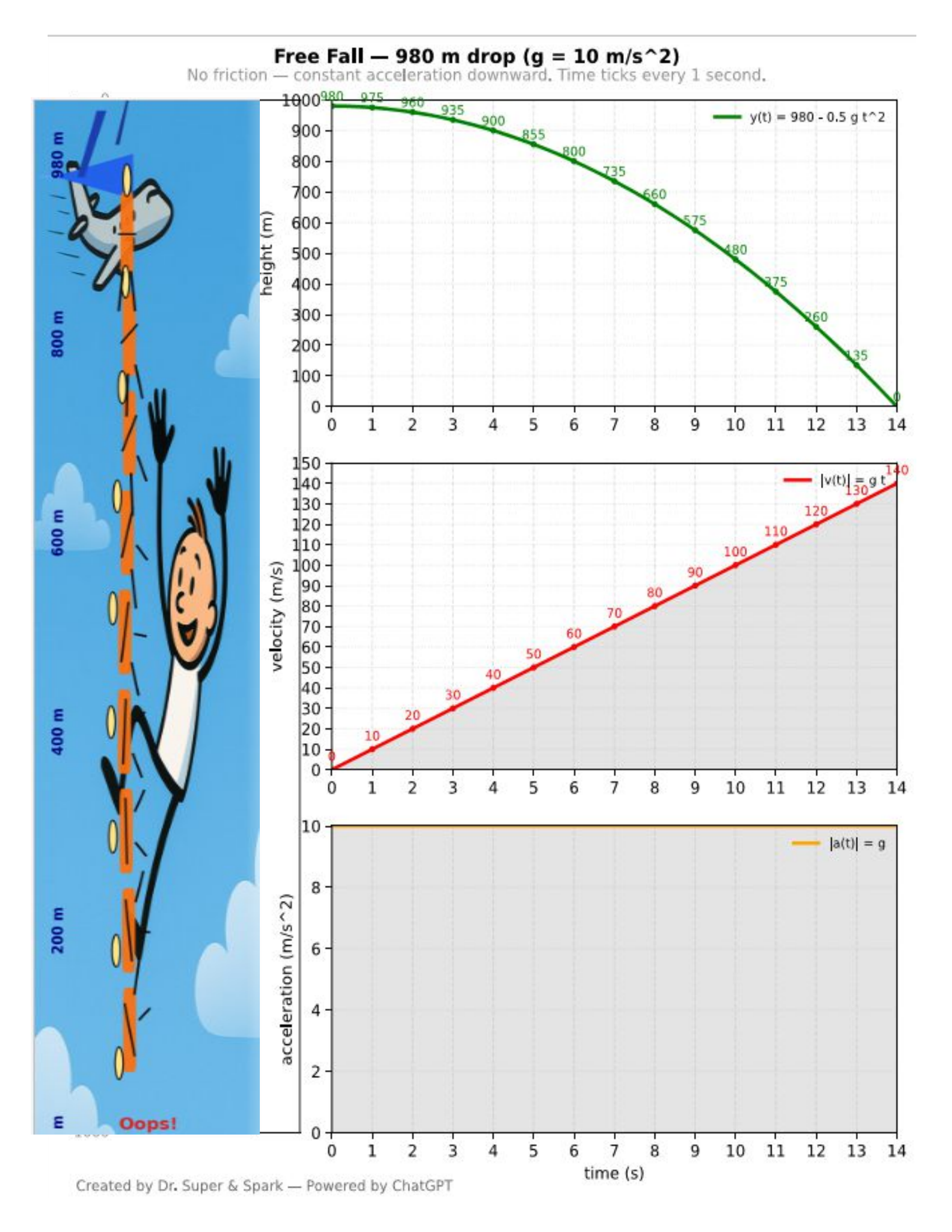
Use the charts. Remember: area under v(t) gives distance fallen, and area under a(t) gives change in velocity. For unit conversion: km/h = (m/s) × 3.6.

Sample solution (g = 10 m/s²)

y(4)=900 m, y(10)=480 m, distance from 4→10 is 420 m
Area under v(t): 0→4 is 80 m, 0→10 is 500 m (matches distance fallen)
Impact: t=14 s, speed = 140 m/s = 504 km/h
Area under a(t) from 4→10: 60 m/s, which equals Δv