🏁 Adventure 5 — Activity

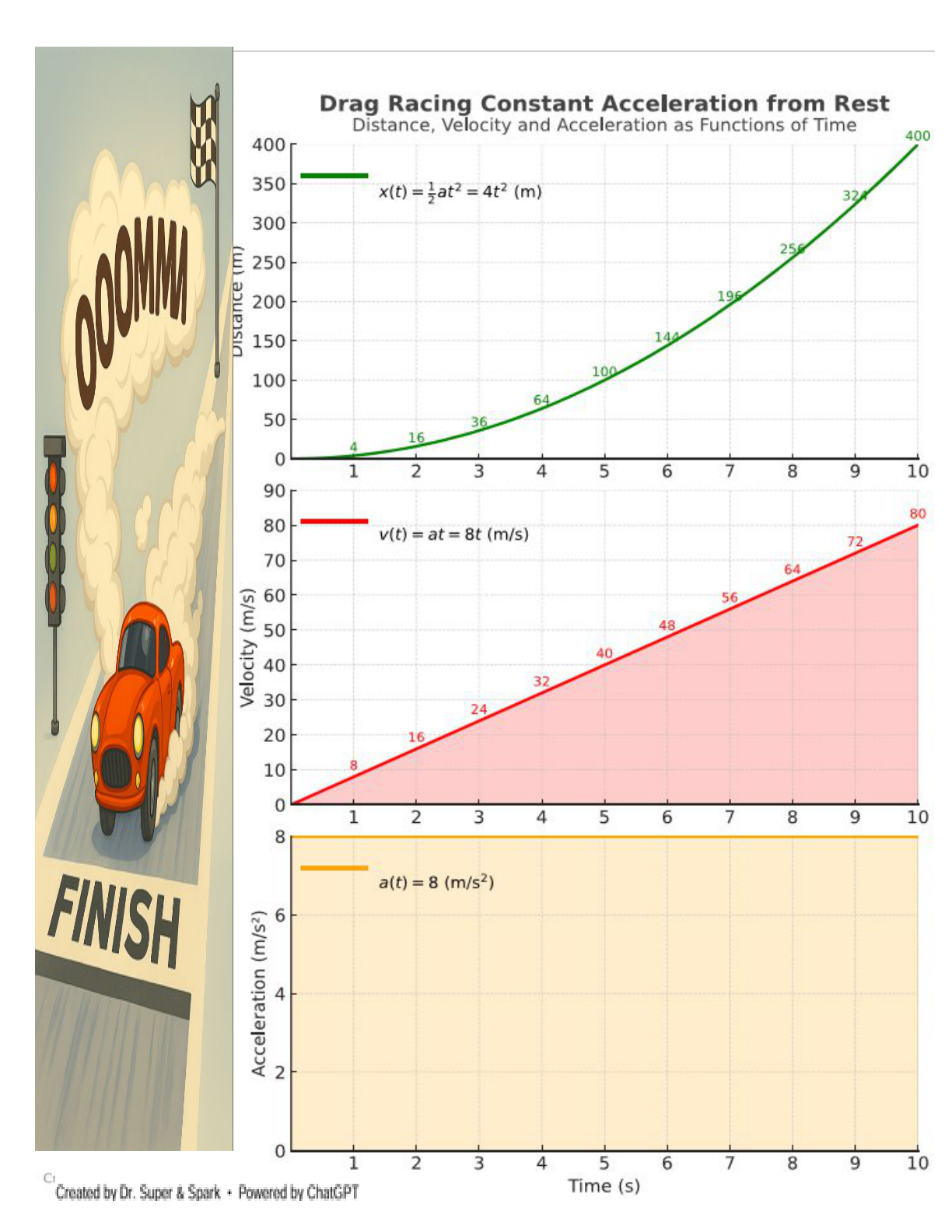
Use the charts to connect distance, velocity, and acceleration — and discover why calculus is really “slope + area”.

Assumptions: no friction • constant acceleration from rest • time ticks every 1 second.

✳ Equations (given)

a(t) = 8 (constant, m/s²)
v(t) = a·t
x(t) = ½·a·t²

1) How far, how fast? (Read the graphs)

Distance after 5 s (m):

Distance after 10 s (m):

Velocity after 5 s (m/s):

Velocity after 10 s (m/s):

2) Area means distance (Area under v(t))

Area under v(t) from 0→5 s (m):

Area under v(t) from 0→10 s (m):

Do these areas match the distances? (Yes/No)

3) Slope means velocity (Tangent line idea)

Slope of tangent to x(t) at t=5 (m/s):

Is this close to v(5)? (Yes/No)

4) Finish line (¼ mile = 400 m)

Time to reach 400 m (s):

Velocity at finish (m/s):

Velocity at finish (km/h):

5) Acceleration check (Area under a(t))

Δv from 0→5 s (m/s):

Δv from 0→10 s (m/s):

Explain (1 sentence):

6) (***) Calculus

Differentiate x(t) to get v(t), then differentiate v(t) to get a(t).
Integrate a(t) to recover v(t), and integrate v(t) to recover x(t).

7) (***) Kinetic Energy and Work

Fill the table to verify KE = ½ m v² matches Work = F·d (for constant acceleration).

Time (s)	Velocity (m/s)	Distance (m)	KE (kJ)	Work (kJ)
2
5
10

Tips: For triangles, area = ½·base·height. For unit conversion: km/h = (m/s) × 3.6.
Remember: area under v(t) gives distance, and area under a(t) gives change in velocity.