✏️ Adventure 6 — Student Activity

Use the chart to connect area to distance and velocity. Motion: speed up, then slow down to a stop (no friction).

✳ Equations of Motion (given)

a(t)=8-2t
v(t)=t(8-t)
s(t)=4t²-(1/3)t³

1) How far, how fast? (Read the distance graph)

Distance traveled in 2 seconds (m):

Distance traveled from 2 to 7 seconds (m):

2) Area means distance (use the velocity curve)

Area under v(t) from 0→2 (m):

Area under v(t) from 2→7 (m):

Are the areas close to the graph read‑offs? (Yes/No)

3) Rectangle estimates (convergence idea)

Estimate total distance from 0→8 seconds by adding rectangles under v(t).

Your estimate with Δt = 1 s (m):

Your estimate with Δt = 0.5 s (m):

Your estimate with Δt = 0.25 s (m):

As Δt gets smaller, your estimate…

4) Velocity as area under acceleration

Signed area under a(t) from 0→8 (m/s):

Velocity at 8 seconds from the velocity graph (m/s):

Are these two numbers equal? (Yes/No)

5) Acceleration check (0→5)

Change in velocity from 0→5 (m/s):

1 sentence: what does area under a(t) mean?

★ Calculus (optional)

s'(t)=v(t) and v'(t)=a(t)
∫v(t)dt gives distance (area idea).

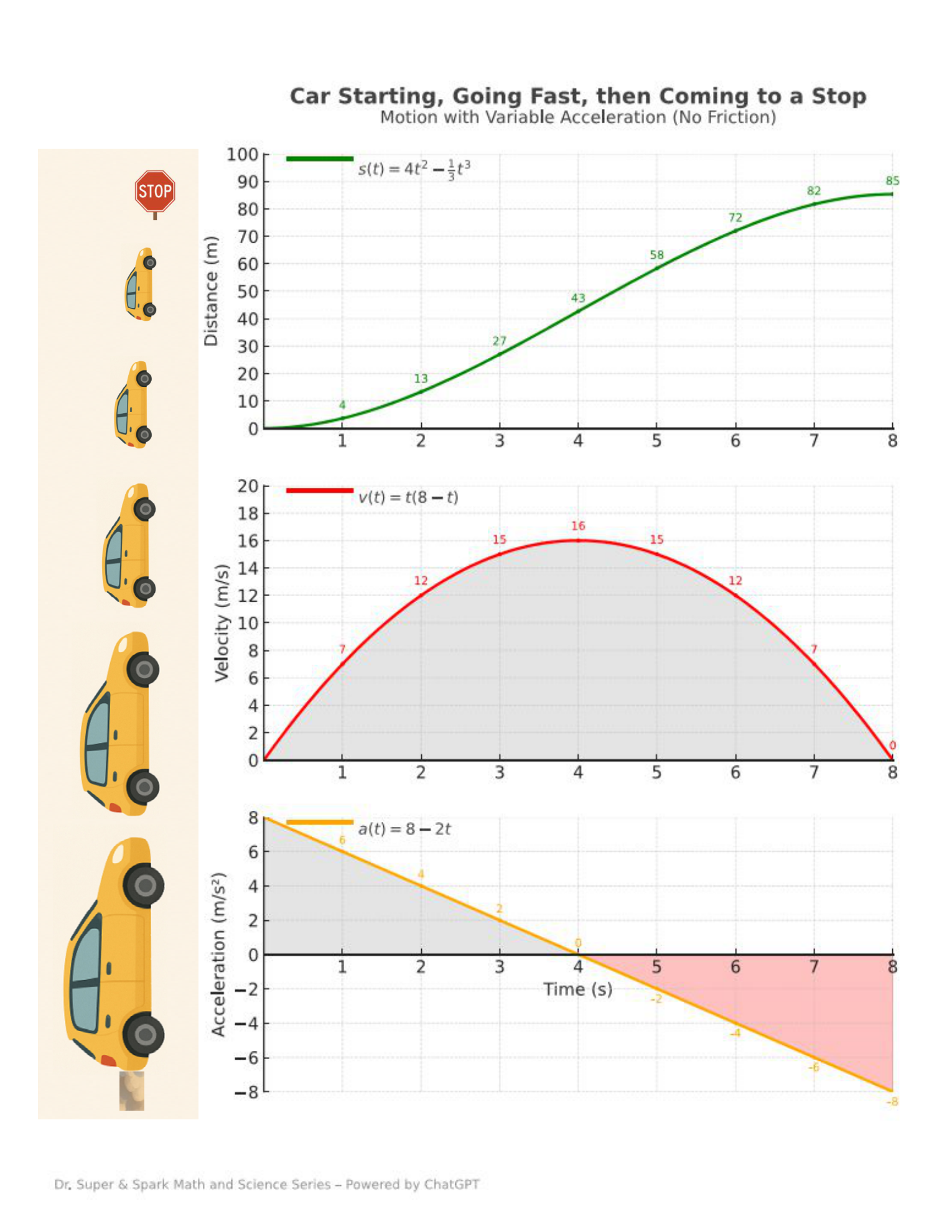
Hint: Area under v(t) is distance. Signed area under a(t) is change in velocity. Use the labels on the curves (values at each second) to estimate.

Reference values

Rectangle totals: Δt=1 → 84.00 m, Δt=0.5 → 85.00 m, Δt=0.25 → 85.25 m
Exact integral (true distance): 85.33 m
Velocity at 8 s: 0 m/s
Change in velocity 0→5: 15 m/s