Adventure 8 — Activity 2: Four DiVA Chart Sets
Compute the two missing equations for each set and use slope/area checks.
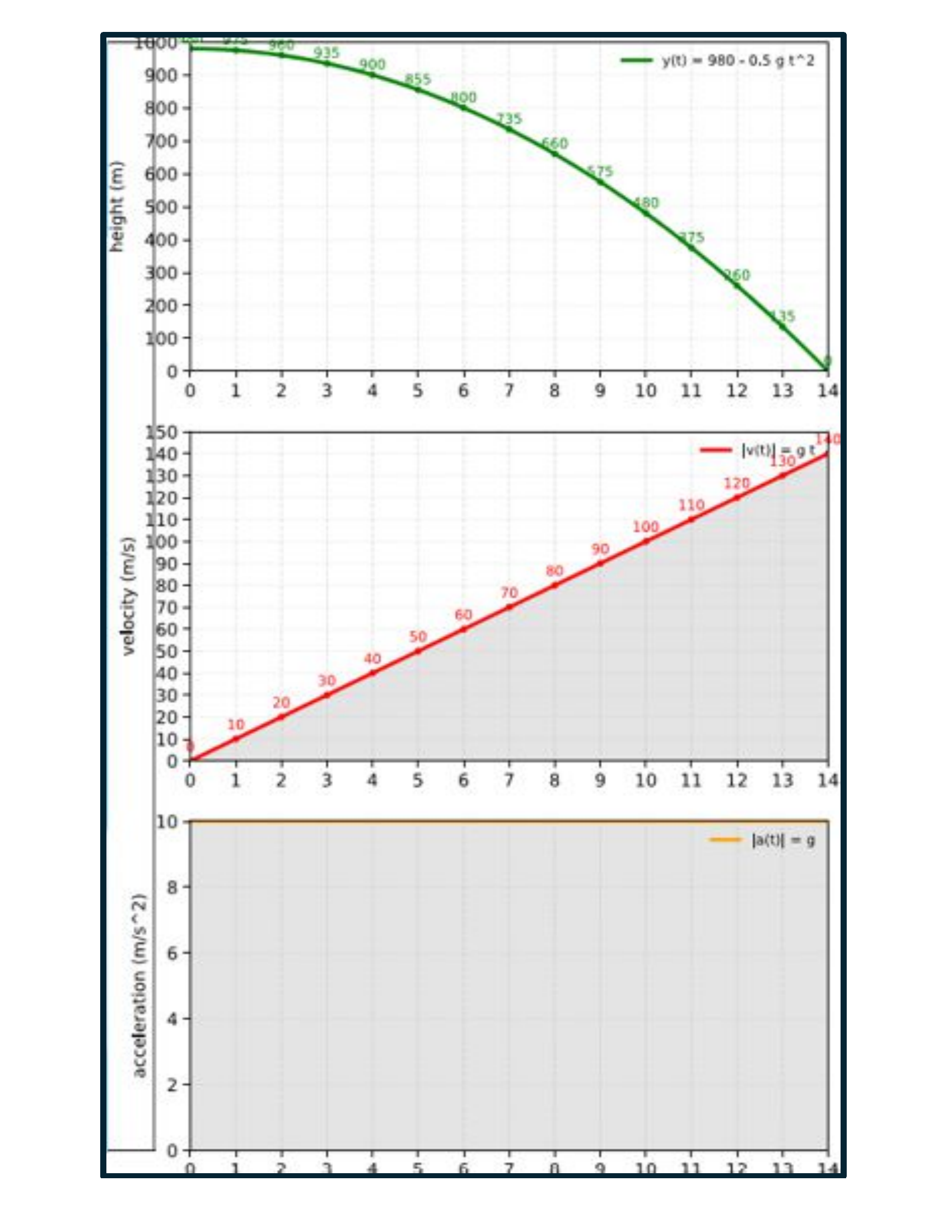
Set 1 — Free Fall (constant acceleration)
Given: Distance (height) function from the graph: y(t) = 980 − 5t² (using g = 10). Find v(t) and a(t) by differentiating.
v(t) =
a(t) =
y(7) =
v(7) =
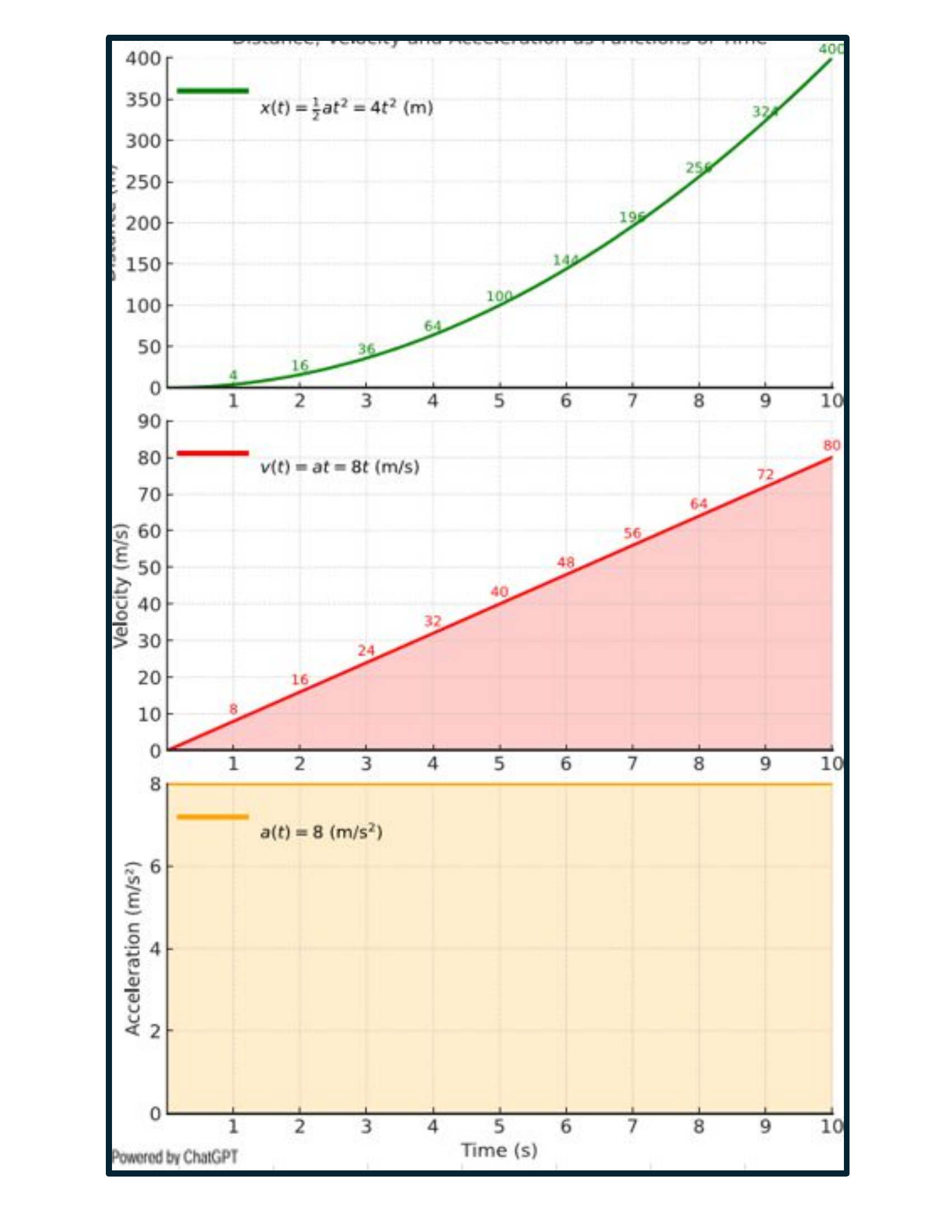
Set 2 — Constant Acceleration a = 8
Given: Constant Acceleration: a = 8. Find x(t) and v(t) by integrating.
Given: Is the slope of v(t) equal to a(t)?
x(t) =
v(t) =
a(t) =
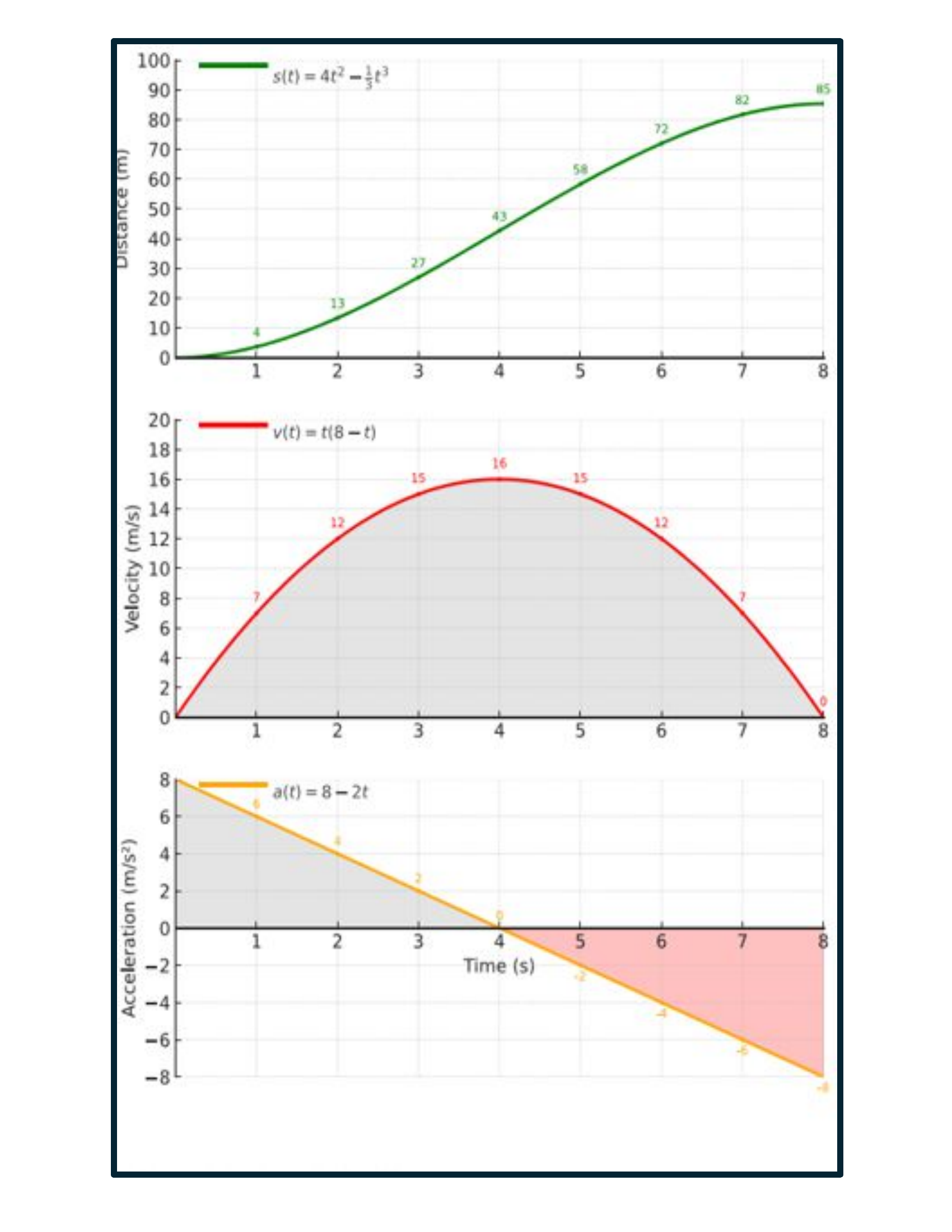
Set 3 — Variable Acceleration
Given: Distance function from the graph: x(t) = 4t² − (1/3)t³. Find v(t) and a(t) by differentiating.
x(t) =
v(t) =
a(t) =
v(4) =
Area under a(t) from 0 to 4 =
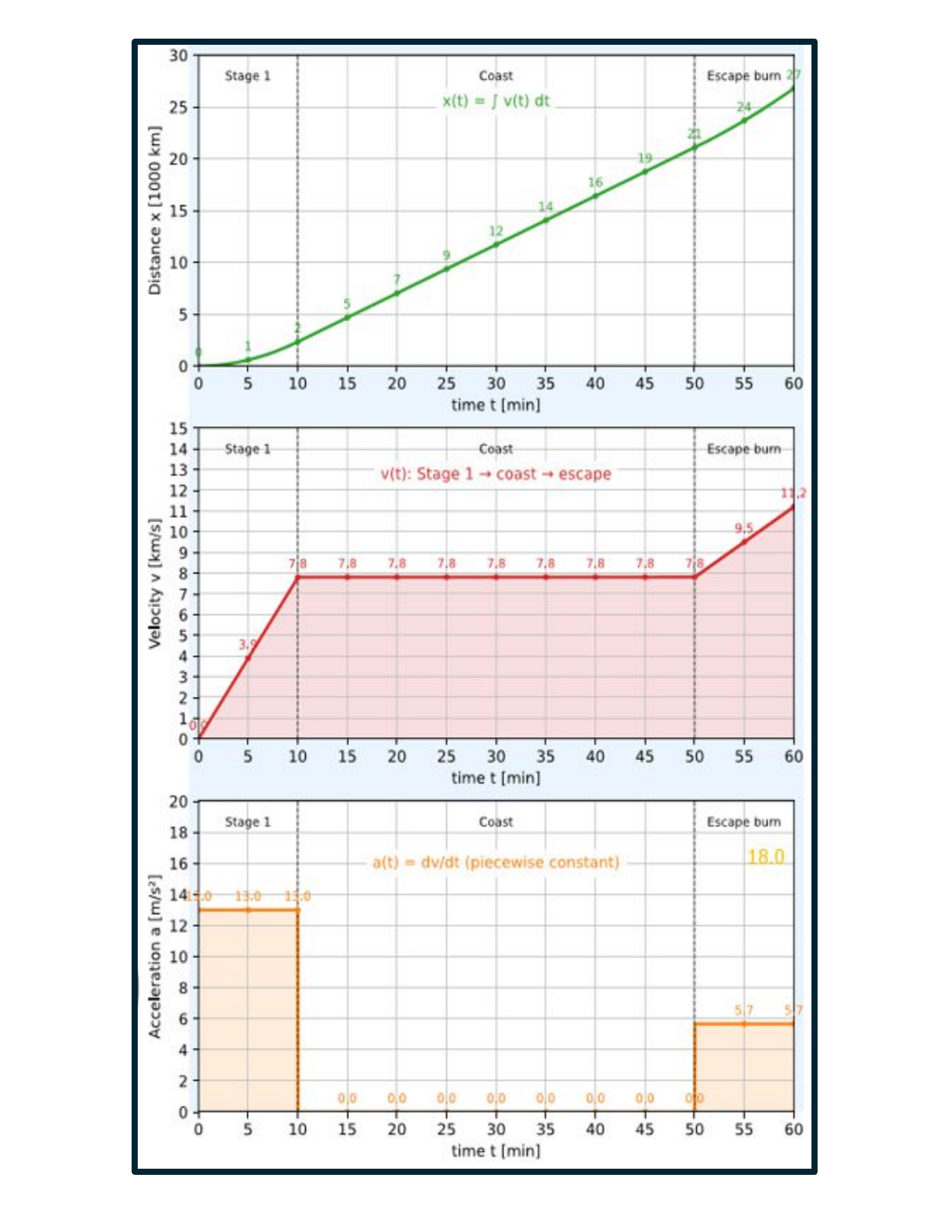
Set 4 — Piecewise Motion (0–10 min, 10–50 min)
Given: Constant Accelaration a: Read a from the chart. Find x(t) and v(t) by integrating.
(0–10 min) x(t) =
(0–10 min) a(t) =
(10–50 min) v(t) =
(10–50 min) a(t) =
x(20 min) =