✏️ Adventure 3 — Activity

Your goal: use geometry to compute df(x), then find df(x)/dx. Keep dx as a tiny number, and remember: terms with dx² and dx³ vanish as dx → 0.

Tip: Think “new pieces only.” The original blue square/cube is already x² or x³.
Only count what gets added when each side grows from x to x + dx.

Part A — Growing a Square: f(x)=x²

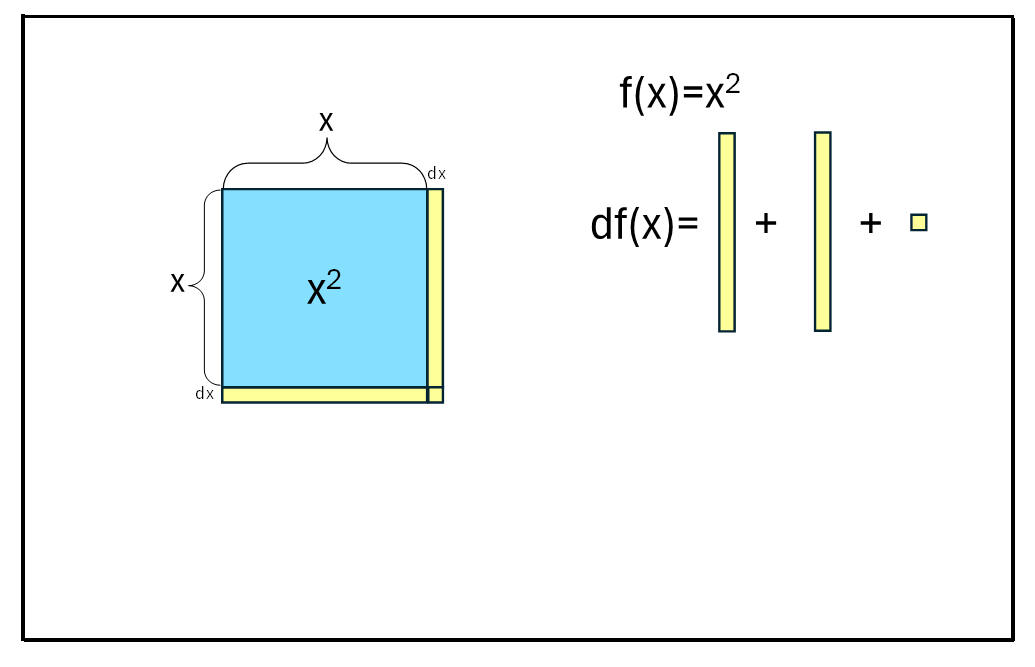
Growing square student image
  1. Write the area of each new piece:
    Vertical strip area =
    Horizontal strip area =
    Corner square area =
  2. Add them to find df(x):
    df(x) =
  3. Simplify:
    df(x) =
  4. Divide by dx:
    df(x)/dx =
  5. Now let dx → 0. Cross out any terms that vanish and write the derivative:
    Derivative: d(x²)/dx =

Part B — Growing a Cube: f(x)=x³

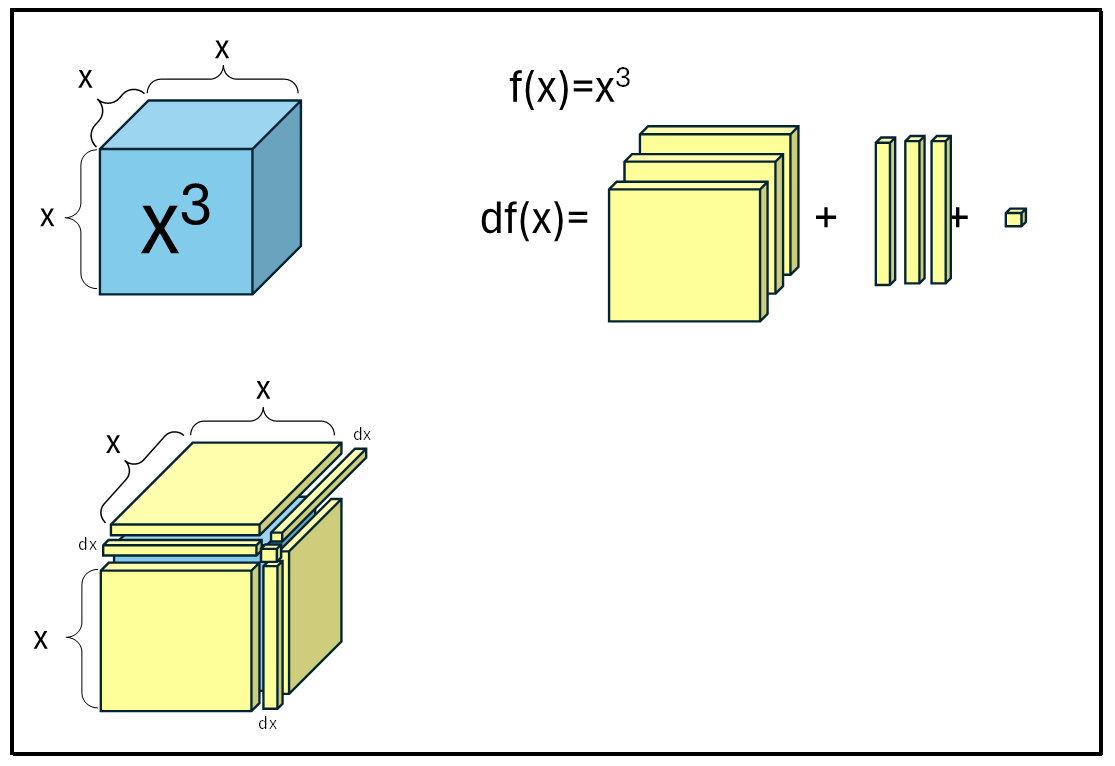
Growing cube student image
  1. List the new pieces that appear when a cube grows from side x to x+dx:
    • How many large face “sheets” of volume x²·dx?
    • How many edge “bars” of volume x·dx²?
    • How many tiny corner cubes of volume dx³?
  2. Add them to find df(x):
    df(x) =
  3. Factor out dx (so dividing is easy):
    df(x) =
  4. Divide by dx:
    df(x)/dx =
  5. Now let dx → 0. Cross out vanishing terms and write the derivative:
    Derivative: d(x³)/dx =

Check: your final answers should be 2x and 3x².