🚀 Adventure 7 — Rocket Launch
Use the two chart sets to connect mass, velocity, momentum, and force.
You will practice slope, area, and the product rule.
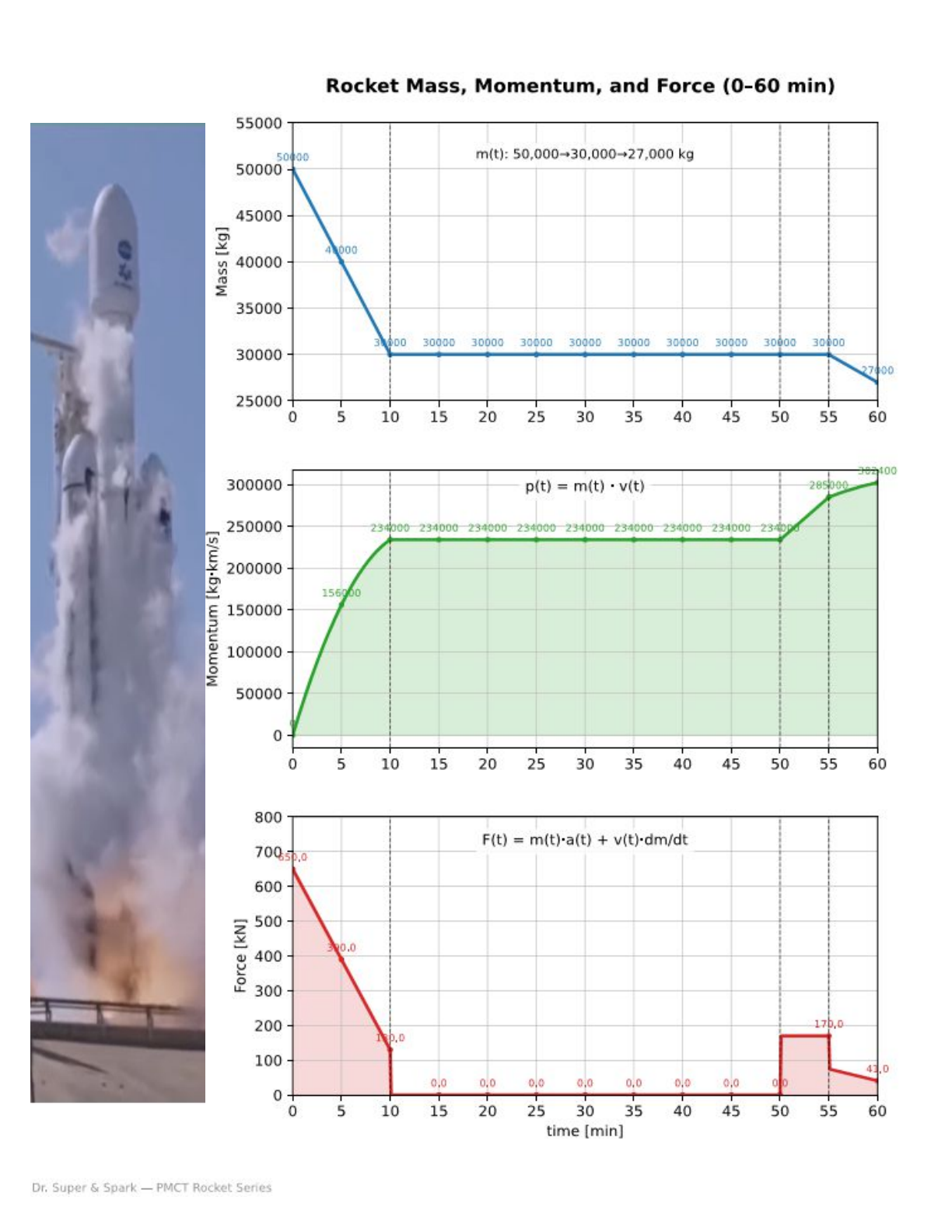
Given: p(t)=m(t)v(t) and F(t)=p′(t)=m(t)a(t)+v(t)m′(t).
Watch units: velocity chart is km/s and must be converted to m/s; mass change is kg/min and must be converted to kg/s.
✳ Equation of Motion (given)
- Mass (kg):
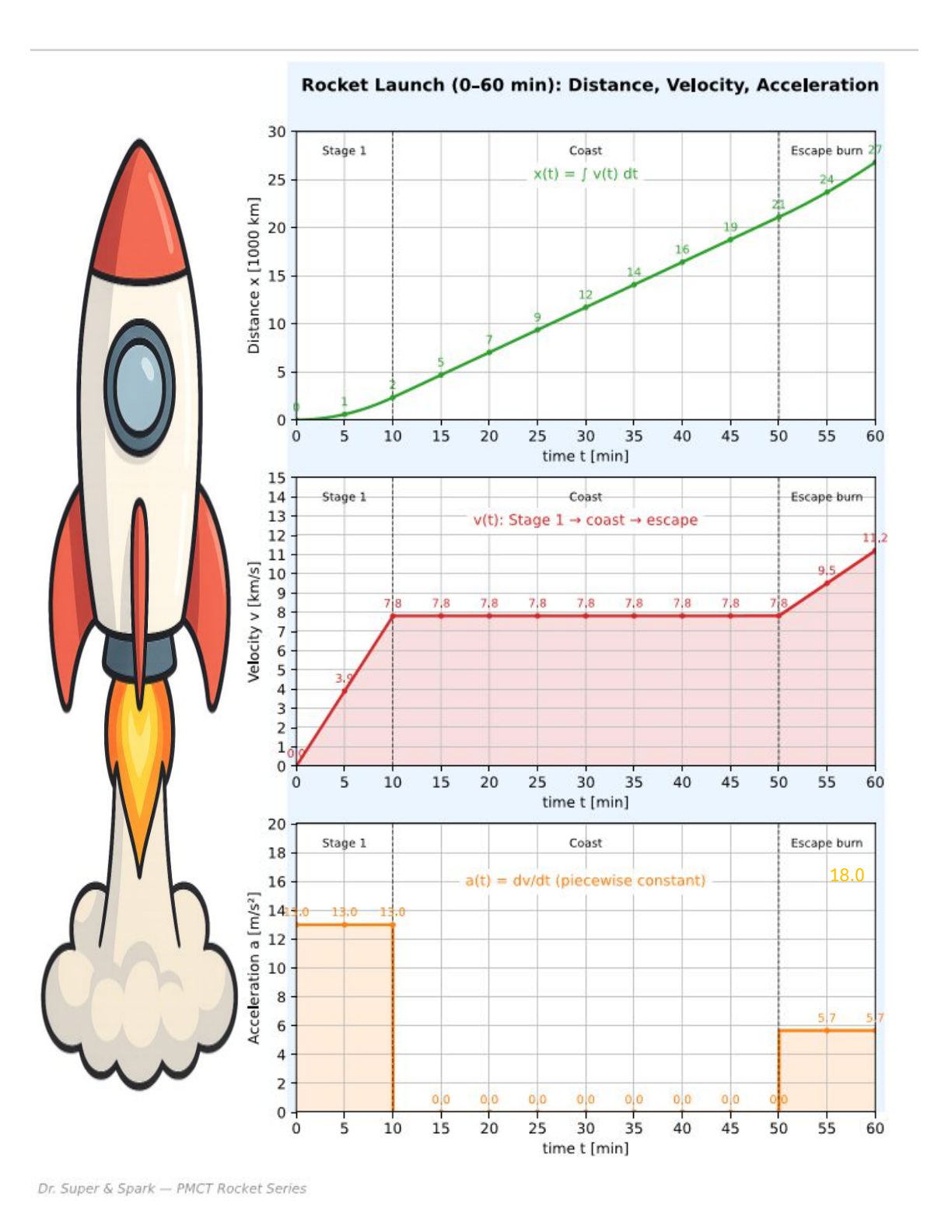
m(t)=50,000−2,000tfor0≤t≤10minm(t)=30,000for10≤t≤55minm(t)=30,000−600(t−55)for55≤t≤60min- Velocity (km/s): read from the red velocity curve.
1) Estimate Velocity from the slope of the distance curve and compare with v(t) chart
Fill the table for t = 5, 30, 58 minutes.
t=5
t=30
t=58
2) Estimate Acceleration from slope of velocity curve and compare with a(t) chart
t=5
t=30
t=58
3) Determine Mass from the mass function
m(5)
m(30)
m(58)
4) Compute mass change m′(t)
t=5
t=30
t=58
5) Compute Force F(t)=m(t)a(t)+v(t)m′(t)
t=5
t=30
t=58
Verify your force values are close to what is shown on the Force chart.
🧠 Interpretation Questions
When is the force largest? Why?
Why is the force close to zero during the coasting phase?
Why does the force increase again near 58 minutes?
★ Challenge
(***) Explain why the slope-estimate for acceleration can match the acceleration chart exactly, but the slope-estimate for velocity from the distance curve is only approximate.
What makes the rocket go forward?
- Convert km/s → m/s by multiplying by 1000.
- Convert kg/min → kg/s by dividing by 60.
- During coasting, acceleration is ~0 and fuel burn is ~0, so force is ~0.
Sample solution ideas:
- Force is largest at launch because acceleration and fuel burn are both high.
- During coasting, the rocket is not burning fuel, so m′(t)=0 and a(t)=0.
- Near 58 minutes, there is a new burn (“escape burn”) giving positive acceleration and fuel loss again.