✅ Adventure 10 — Solutions
Answer key for the Feynman–Gamow Mission (ratios + DiVA + visual L’Hôpital).
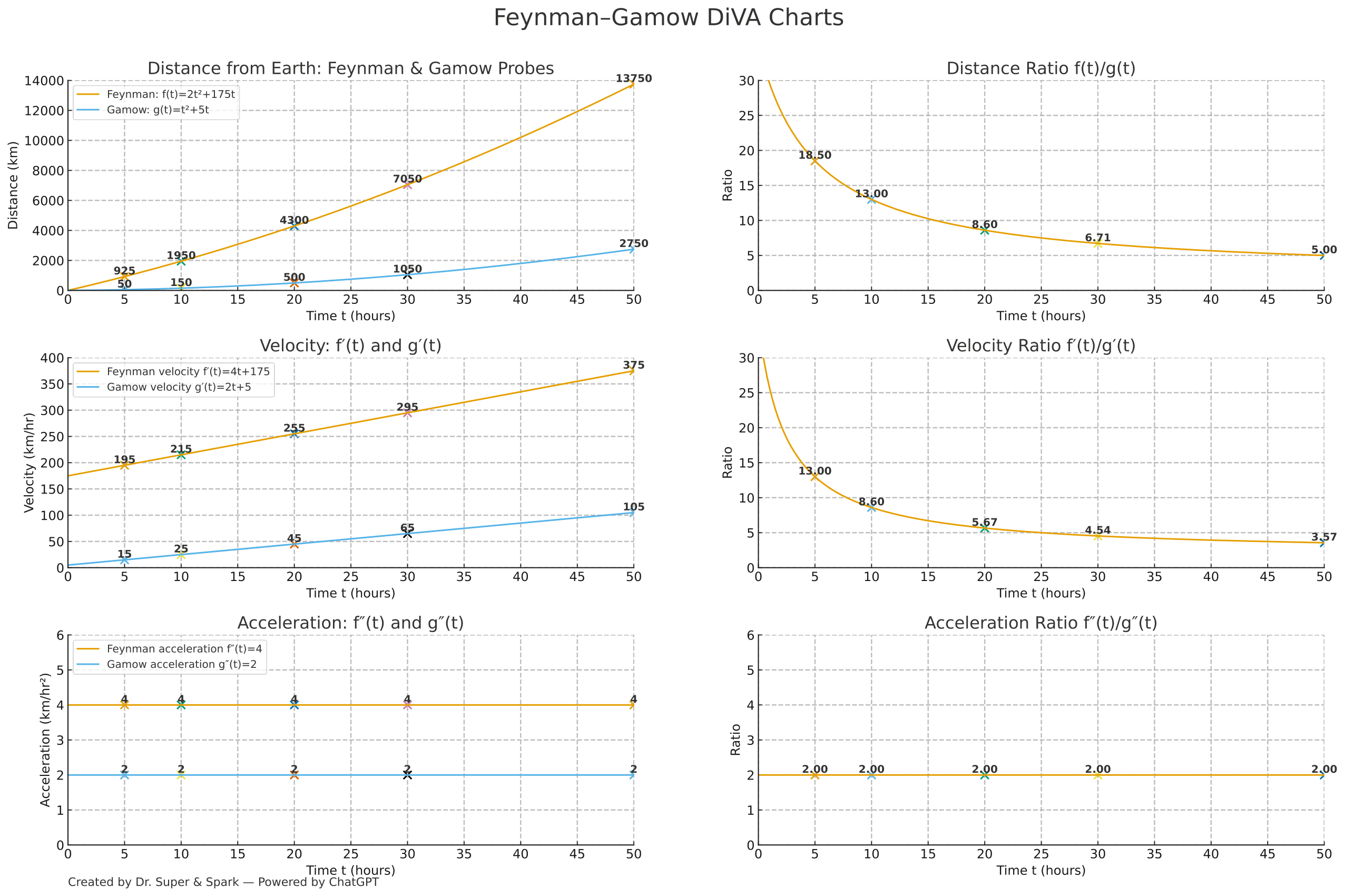
1) Mission rule
- Rule:
f(t)/g(t) ≥ 2for all mission timest ≥ 0. - Meaning: Feynman must stay at least twice as far from Earth as Gamow so Gamow’s radio does not interfere with Feynman’s sensitive measurements.
2) Derivatives
f'(t)=4t+175,g'(t)=2t+5f''(t)=4,g''(t)=2- Acceleration ratio:
f''(t)/g''(t)=4/2=2(constant)
3) Distance ratios at marked times
| t (hours) | f(t) | g(t) | f(t)/g(t) |
|---|---|---|---|
| 5 | 925 | 50 | 18.50 |
| 10 | 1,950 | 150 | 13.00 |
| 20 | 4,300 | 500 | 8.60 |
| 30 | 7,050 | 1,050 | 6.71 |
| 50 | 13,750 | 2,750 | 5.00 |
4) Long‑time ratios
| t (hours) | Distance ratio f(t)/g(t) | Velocity ratio f'(t)/g'(t) |
|---|---|---|
| 240 | 2.67 | 2.34 |
| 720 | 2.23 | 2.11 |
| 1200 | 2.14 | 2.07 |
Conclusion: As t → ∞, both distance and velocity ratios approach 2.
5) Chain reaction explanation
- Since
f''/g'' = 2forever, that’s the “target” long‑term ratio. - The constants in
f'(t)=4t+175andg'(t)=2t+5matter early, but become less important astgrows. - So the velocity ratio approaches 2, and because distance is the accumulated area under velocity, the distance ratio also approaches 2 (from above).
6) Mission explanation
Both probe distances grow without bound, but the ratio f(t)/g(t) drops toward 2 and never goes below it. The acceleration ratio is constant at 2, which forces the velocity ratio toward 2, and that forces the distance ratio toward 2. DiVA makes this “L’Hôpital idea” visible: each derivative step simplifies the long‑term comparison.
⭐ Challenge
For same‑degree polynomials, the ratio approaches the ratio of the leading coefficients. In the provided challenge, that limiting ratio is 3.