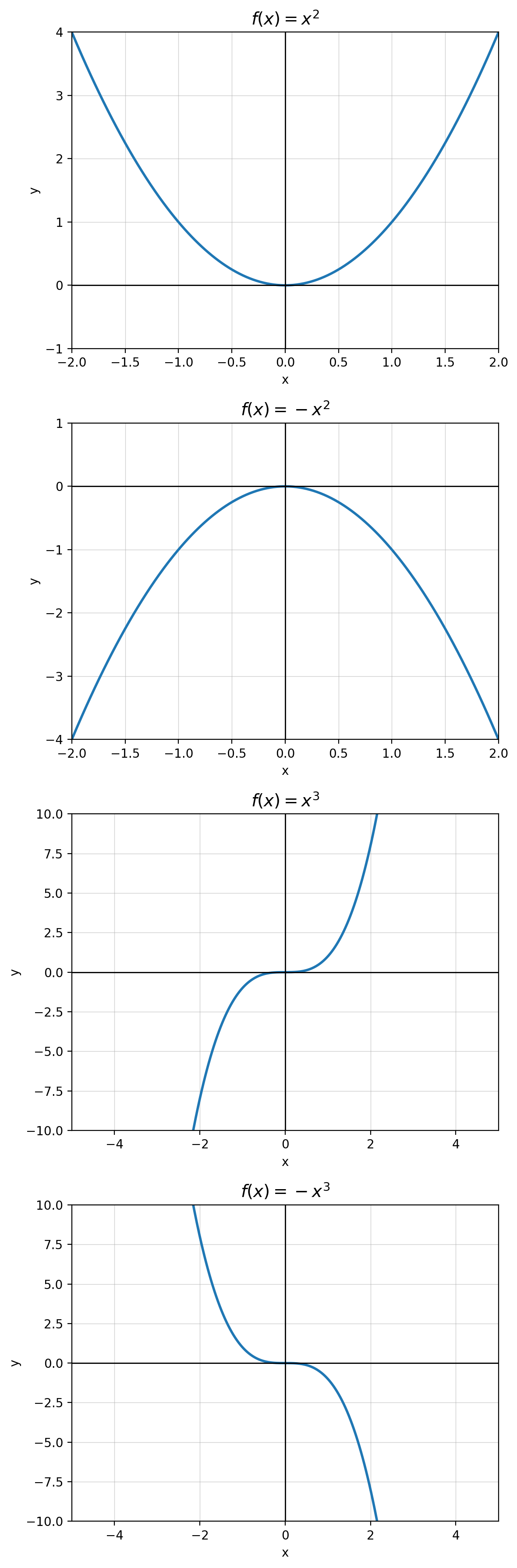
🧩 Adventure 13 — Activity 1
Training with four functions:
x², −x², x³, −x³
Goal: For each function, compute
f, f′, and f″ at x = −2, −1, 0, 1, 2.
Then decide: does the point (0,0) give a maximum, minimum, or an inflection point?
1) f(x) = x²
Compute derivatives:
f′(x) =
f″(x) =
| x | f | f′ | f″ |
|---|---|---|---|
| -2 | |||
| -1 | |||
| 0 | |||
| 1 | |||
| 2 |
2) f(x) = −x²
f′(x) =
f″(x) =
| x | f | f′ | f″ |
|---|---|---|---|
| -2 | |||
| -1 | |||
| 0 | |||
| 1 | |||
| 2 |
3) f(x) = x³
f′(x) =
f″(x) =
| x | f | f′ | f″ |
|---|---|---|---|
| -2 | |||
| -1 | |||
| 0 | |||
| 1 | |||
| 2 |
4) f(x) = −x³
f′(x) =
f″(x) =
| x | f | f′ | f″ |
|---|---|---|---|
| -2 | |||
| -1 | |||
| 0 | |||
| 1 | |||
| 2 |
Finish: Use your tables to complete these statements:
- For
x², we have a ________ at (0,0) becausef′(0)=___ andf″(0)is ________. - For
−x², we have a ________ at (0,0) becausef′(0)=___ andf″(0)is ________. - For
x³, we have an ________ at (0,0) becausef″(0)=___ and the concavity changes. - For
−x³, we have an ________ at (0,0) becausef″(0)=___ and the concavity changes.