🎯 Adventure 13 — Activity 2 (Solution)
DiVA reasoning with D(t) given
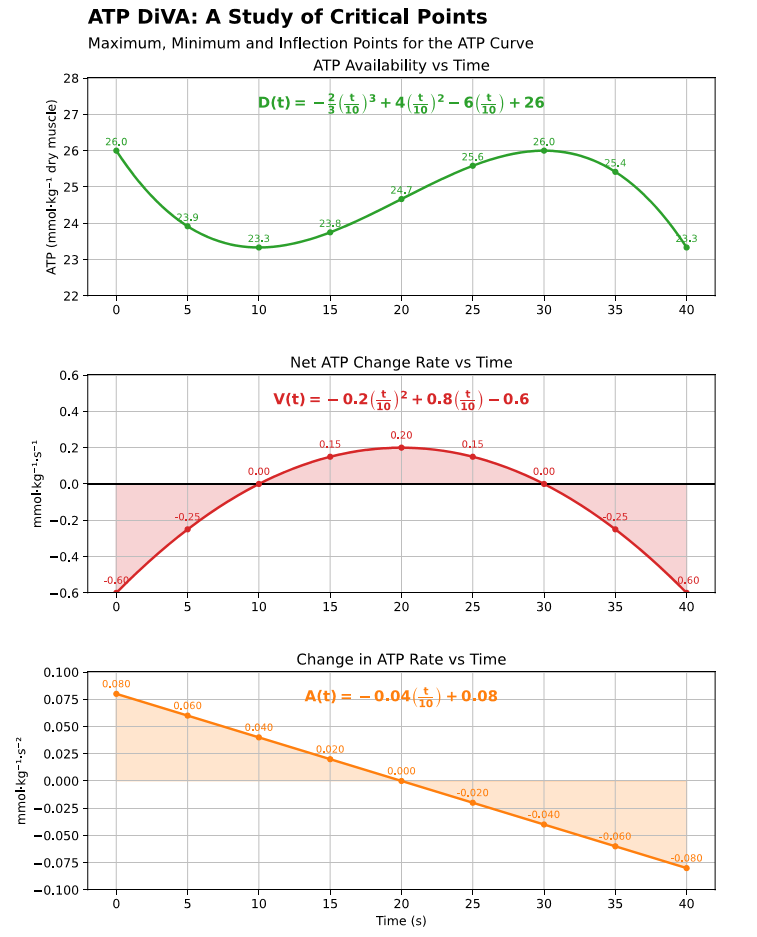
Solution: Use derivatives to locate min/max and the inflection point, then sketch D(t).
1) Derivatives
V(t)=D′(t)= −2t² + 80t − 600
A(t)=V′(t)=D″(t)= −4t + 80
2) Critical points for D(t)
- Solve V(t)=0 → t=10 and t=30
- D″(10)=40>0 → minimum at t=10
- D″(30)=−40<0 → maximum at t=30
- Inflection point: A(t)=0 → t=20
3) Helpful values
| t | D(t) | V(t) | A(t) |
|---|---|---|---|
| 0 | 26000 | -600 | 80 |
| 10 | 23333.33 | 0 | 40 |
| 20 | 24666.67 | 200 | 0 |
| 30 | 26000 | 0 | -40 |
| 40 | 23333.33 | -600 | -80 |
4) Reasoning statements
- When A(t)>0, V(t) is increasing.
- When V(t)>0, D(t) is increasing.
- V(t) reaches its maximum at t=20 (because A(t)=0 and changes sign).
Given (simplified units)
D(t) = −(2/3)t³ + 40t² − 600t + 26,000
V(t)=D′ = −2t² + 80t − 600
A(t)=V′=D″ = −4t + 80
Table 1. Sign Table for Drawing D (ATP Availability)
| Interval (seconds) | 0–10 | 10 | 10–20 | 20 | 20–30 | 30 | 30–40 |
|---|---|---|---|---|---|---|---|
| D (ATP availability) | − | min | + | Inflection | + | max | − |
| V = D′ | − | 0 | + | + | + | 0 | − |
| A = V′ = D″ | + | + | + | 0 | − | − | − |
▭(V(t)=−2t²+80t−600) ▭(A(t)=−4t+80)
Table 2. Values for V(t) and A(t)
| t | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
|---|---|---|---|---|---|---|---|---|---|
| V(t) | -600 | 250 | 0 | 150 | 200 | 150 | 0 | 250 | -600 |
| A(t) | 80 | 60 | 40 | 20 | 0 | -20 | -40 | -60 | -80 |
Use the values in Table 2 to put signs in Table 1.
First derivative decides if there is an extremum (max/min). Second derivative decides which kind.
At t=10 we have a minimum since V(10)=0 and A(10)=40>0.
At t=30 we have a maximum since V(30)=0 and A(30)=−40<0.
At t=20 we have an inflection point since A(20)=0.
First derivative decides if there is an extremum (max/min). Second derivative decides which kind.
At t=10 we have a minimum since V(10)=0 and A(10)=40>0.
At t=30 we have a maximum since V(30)=0 and A(30)=−40<0.
At t=20 we have an inflection point since A(20)=0.
Table 3. Values for D(t)
| t | 0 | 10 | 20 | 30 | 40 |
|---|---|---|---|---|---|
| D(t) | 26,000 | 23,333 | 24,666 | 26,000 | 23,333 |
▭(D(t)=−2/3 t³ + 40t² − 600t + 26,000)
D(0)=26,000 D(10)=23,333 D(20)=24,666 D(30)=26,000 D(40)=23,333
D(0)=26,000 D(10)=23,333 D(20)=24,666 D(30)=26,000 D(40)=23,333
Sketch notes
- On the top graph of the DiVA: mark where V(t)=0 (min/max).
- Mark where A(t)=0 (inflection).
- Use Table 1 and Table 3 to draw a smooth, reasoned sketch.
The Parting Shot
You can sketch the function’s shape using only the critical points (zeros of V), the inflection point (zero of A),
and the signs. This is powerful because calculus lets you understand the whole curve without plotting lots of points.