🧩 Adventure 13 — Activity 2

DiVA reasoning (no curve-drawing for V and A)

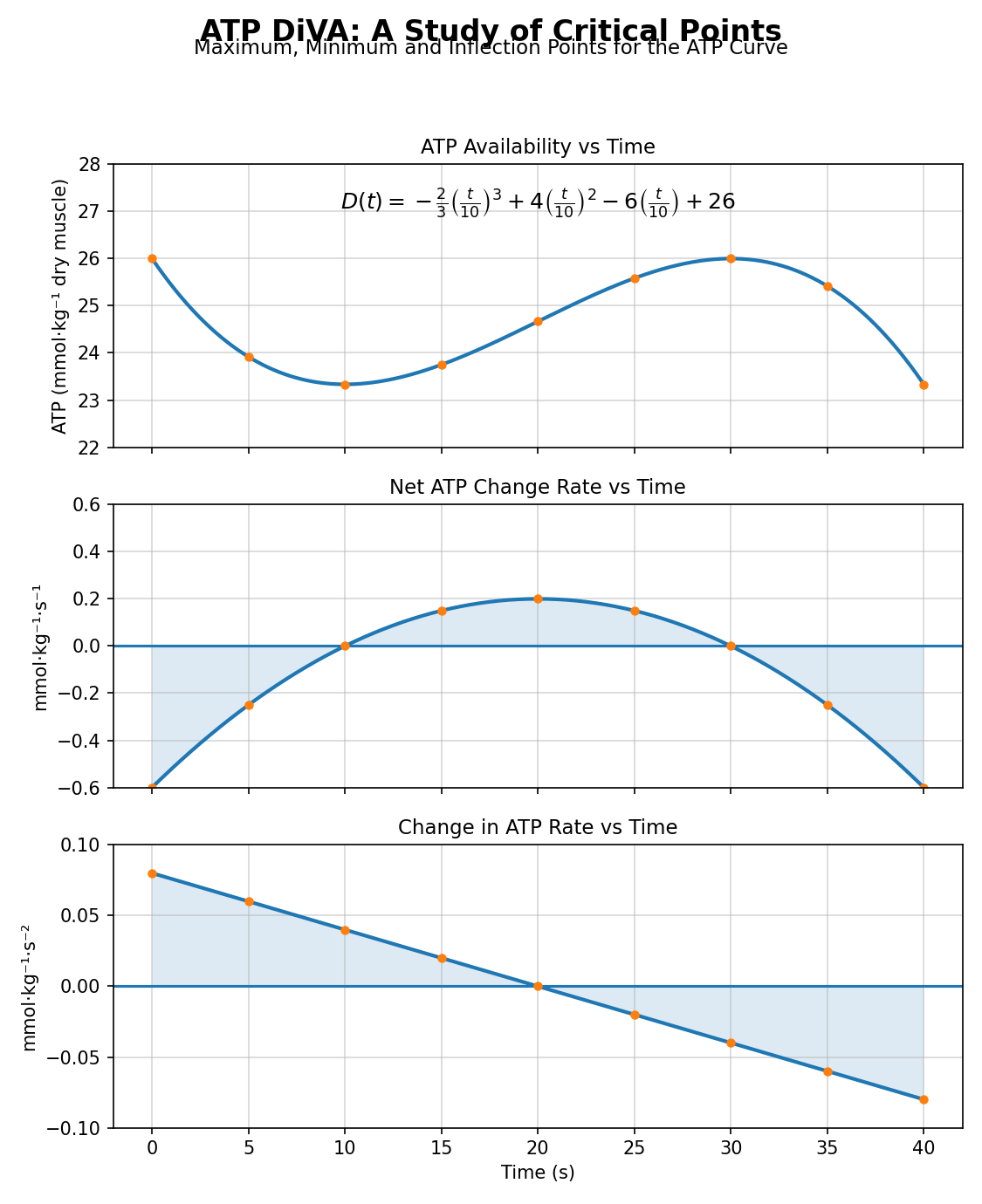
ATP DiVA reference (curves + shading; D(t) only)

Goal: Build the ATP availability curve D(t) using calculus — derivatives, sign tables, and a few values. You will sketch D(t) on the DiVA chart using critical points (max/min) and an inflection point.

Given (simplified units)

D(t) = −(2/3)t³ + 40t² − 600t + 26,000

V(t)=D′ = −2t² + 80t − 600

A(t)=V′=D″ = −4t + 80

Part 1 — Compute the derivatives

V(t) = D′(t) =

A(t) = V′(t) = D″(t) =

Part 2 — Critical points for D(t)

1) Solve V(t)=0 to find where D(t) has a maximum or minimum.

t values: t₁ = t₂ =

2) Use A(t)=D″(t) to decide which is a max and which is a min.

D(t) has a minimum at t = and a maximum at t =

3) Inflection point for D(t): solve A(t)=0.

Inflection time: t =

Part 3 — Reasoning about V(t) and A(t)

When A(t) is positive, V(t) is (increasing / decreasing) →
When V(t) is positive, D(t) is (increasing / decreasing) →
Where does V(t) reach its maximum? (Hint: A(t)=0) → t =

Important idea: You can understand max/min/inflection without sketching the whole curve — if you know how the derivatives behave.

Part 4 — Sign table (structure)

You will use signs of V and A to decide where D is decreasing/increasing and where it has min/max/inflection.

Interval (seconds)	0–10	10	10–20	20	20–30	30	30–40
D (ATP availability)
V = D′
A = V′ = D″

Table 2 — Values for V(t) and A(t)

Use V(t) and A(t) formulas to compute values. Then use the sign of each value to fill Table 1.

t	0	5	10	15	20	25	30	35	40
V(t)
A(t)

Critical points from derivatives

First derivative decides if there is an extremum (max/min). Second derivative decides which kind. Also, an inflection happens when A(t)=D″(t)=0 (and the concavity changes).

At t = 10 we have a because V(10)=0 and A(10) is .

At t = 30 we have a because V(30)=0 and A(30) is .

At t = 20 we have an because A(20)=0.

Table 3 — Values for D(t)

Compute D(t) at these times (or use your calculator). These values help anchor your sketch.

t	0	10	20	30	40
D(t)

Part 5 — Sketch the ATP Availability Curve

On the top graph of the DiVA, mark where V(t)=0 (min/max).
Mark where A(t)=0 (inflection).
Use Table 1 (signs) and Table 3 (values) to draw a smooth, reasoned sketch.

Part 6 — Compare with the ChatGPT DiVA

My chart is very similar to the DiVA Charts produced by ChatGPT: Yes No

Explain what is happening with ATP availability:

Part 7 — The Parting Shot

Without recalculating any values: explain how you could sketch the shape of the ATP curve using only zeros of V(t), zeros of A(t), and signs. Why is this a powerful idea in calculus?